In a previous couple of articles, we explored some basic machine learning algorithms and how they fit into the .NET world. Thus far we covered some simple regression algorithms, classification algorithms. Apart from that, we learned a bit about unsupervised learning, more specifically – clustering. We used ML.NET to implement and apply these algorithms. In the previous article, we learned about SVM, an algorithm that can be used for regression and for classification. We continue down that path and explore one more universal and one of the most popular machine learning algorithms – Decision Trees.
Are you afraid that AI might take your job? Make sure you are the one who is building it.
STAY RELEVANT IN THE RISING AI INDUSTRY! 🖖
The topics covered in this article are:
1. Dataset and Prerequisites
Data that we use in this article is from PalmerPenguins Dataset. This dataset has been recently introduced as an alternative to the famous Iris dataset. It is created by Dr. Kristen Gorman and the Palmer Station, Antarctica LTER. You can obtain this dataset here, or via Kaggle. This dataset is essentially composed of two datasets, each containing data of 344 penguins. Just like in Iris dataset there are 3 different species of penguins coming from 3 islands in the Palmer Archipelago. Also, these datasets contain culmen dimensions for each species. The culmen is the upper ridge of a bird’s bill. In the simplified penguin’s data, culmen length and depth are renamed as variables culmen_length_mm and culmen_depth_mm.

Data itself is not too complicated. In essence, it is just tabular data:

Note that in this tutorial, we ignore the species feature. This is because we perform unsupervised learning, ie. we don’t need the expected output value of the sample. We want our algorithm to figure that out on its own. Here is how data looks like when we plot it:

For the regression examples in this article, we use the famous Boston Housing Dataset. This dataset is composed of 12 features and contains information collected by the U.S Census Service concerning housing in the area of Boston Mass. It is a small dataset with only 506 samples.

The complete dataset looks somewhat like this:

In fact, most of the features in this dataset have almost linear dependency:

The implementations provided here are done in C#, and we use the latest .NET 5. So make sure that you have installed this SDK. If you are using Visual Studio this comes with version 16.8.3. Also, make sure that you have installed the following package:
Install-Package Microsoft.ML.FastTreeNote that this will install default Microsoft.ML package as well. You can do a similar thing using Visual Studio’s Manage NuGetPackage option:

If you need to catch up with the basics of machine learning with ML.NET check out this article.
2. Decision Trees Intuition
In essence, Decision Tree is a set of algorithms, because there are multiple ways in which we can solve this problem. Some of the most famous ones are:
- CART
- ID3
- C4.5
- C5.0
In this article, we focus on the CART algorithm which is easies and one of the most popular ones. Among others, the Sci-Kit Learn library uses this algorithm under the hood. This algorithm produces a binary tree, which might not be the case with other algorithms. This means that the node is either branching in two nodes or it is not branching at all (terminal node or terminal leaf). Here is the preview of how CART builds a Decision Tree.

In the beginning, it adds the root node of the three and we push all data to it. In this first node, we examine the value of one of the features. In the example of PalmerPenguins let’s say it examines culmen_length_mm feature and compares it with the chosen threshold, in this case, 42.55. Thus, data is partitioned into two sets. The first one for which this question is true, and the other one for which it is not. Then two new nodes are created which are examining some other feature and uses some other thresholds:

The process is then repeated. The depth of the tree is controlled by the max_depth hyperparameter. How the thresholds are created? To understand that we need to explain two important concepts: impurity and information gain. Impurity can be defined as a chance of being incorrect if you assign a label to an example by random. This means that a node is “pure” if all training instances it applies to belong to the same class, meaning when you assign a label to a random sample you can not make a mistake. There are different ways for measuring impurity such a Gini index and entropy. In this article, we use the Gini index. To calculate Gini impurity index we use the formula:
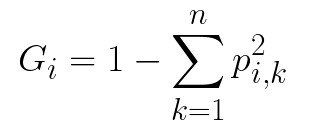
where pi,k is the ratio of class k instances among the training instances in the i-th node. For example, if we have 43 instances of the training set in the node of which 13 belong to one class, while 30 instances belong to a second class. Given that we have only those two classes in the training dataset, we calculate Gini impurity 1 – (13/43)2 – (30/43)2 ≈ 1 – 0.09 – 0.49 ≈ 0.42. When the node is “pure” its Gini index is 0.
On the other hand, information gain lets us find the best threshold which will reduce this impurity the most. To calculate information gain we need to calculate average impurity and then subtract that from the starting impurity. That is how we know the quality of thresholds that we used.
Based on these two concepts we can define how the CART algorithm functions. In its essence, it is a greedy algorithm that repeats the process for each level (depth). First, it splits the training dataset into two subsets using single feature j and a threshold tj. The feature and the threshold are picked like that so that they produce the purest subsets weighted by their size. The cost function that CART minimizes can be defined as:

where ml and mr represent the number of instances in the respective side (right, left), m is the total number of instances and Gl and Gr represent the Gini impurity index on the respective side. Once this is done, it does the same to each subset. The process is repeated recursively until the maximum depth is reached or a split that reduces impurity can not be found. This algorithm can be used for both regressions and for classification. The only difference is that in one case the resulting decision is the class of the sample, while in the other is the value of the sample. Also, instead of trying to reduce the Gini impurity index, for regression tasks MSE (mean squared error) is used:
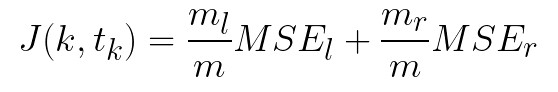
Visually, this decision tree looks something like this:

3. ML.NET Supported Decision Trees Algorithms
ML.NET supports several variations of Decision Trees for both classification and regression. Unfortunately, classification variations are limited only to binary classification. We hope that in the future, we will get an option to perform multiclass classification as well. Here are the available algorithms in ML.NET:
- Fast Tree – This is an implementation of so called MART algorithm, which is known to deliver high prediction accuracy for diverse tasks, and it is widely used in practice. Multiple Additive Regression Trees (MART) is an ensemble model of boosted regression trees, which essentially means it uses gradient boost as a part of its calculations. This algorithm builds each regression tree in a step-wise fashion, using a predefined loss function to measure the error for each step and corrects it in the next. In the end, we actually have an ensemble of weaker prediction models. In regression problems, boosting builds a series of such trees in a step-wise fashion and then selects the optimal tree using the loss function.
- Fast Tree Tweedie – In essence, it is similar to the previous algorithm, but it uses a different gradient boosting algorithm. This algorithm follows the mathematics established in Insurance Premium Prediction via Gradient Tree-Boosted Tweedie Compound Poisson Models from Yang, Quan, and Zou.
- GAM – Even though Generative Additive Models (GAM) are not Decision Trees model, they are usually implemented with Decision Trees so they are explored in the same context. GAM threats the data as a set of linearly independent features. Then for each feature, it learns a non-linear function (shape function), that computes the response as a function of the feature’s value. To score an input, the outputs of all the shape functions are summed and the score is the total value. Decision Trees are used to learn those shape functions and eventually build the GAM model.
Note that Fast Tree and GAM algorithms have their respective binary classification and regression variations, while Fast Tree Tweedie is available only for regression problems. First, we consider classification examples.
4. Classification Implementation with ML.NET
ML.NET currently supports only binary classification with Decision Trees. As you are probably aware, binary classification is performing simple classification on two classes. In essence, it is used for detecting if some sample represented some event or not. So, simple true-false predictions, which can be quite useful. That is why we need to modify and pre-process data from PalmerPenguin Dataset. We left two features culmen depth and culmen length. The other features are removed. We also modify the species feature, which now indicated if the sample belongs to the Adelie species or not (1 if the sample represents Adelie; 0 otherwise). Here is how data looks like now:

This is a simplified dataset and the problem we want to learn – Does some new sample that comes in our system represents Adelie’s class or not. Here is what that means for our dataset visually:

4.1 High-Level Architecutre
Before we dive deeper into this implementation, let’s consider the high-level architecture of this implementation. In general, we want to build an easily extendable solution that we can easily extend with new Decision Trees algorithms that ML.NET will hopefully include in the future. We certainly hope that multiclass options will be available in the future. That is why the folder structure of our solution looks like this:

The Data folder contains .csv with input data and the MachineLearning folder contains everything that is necessary for our algorithm to work. The architectural overview can be represented like this:
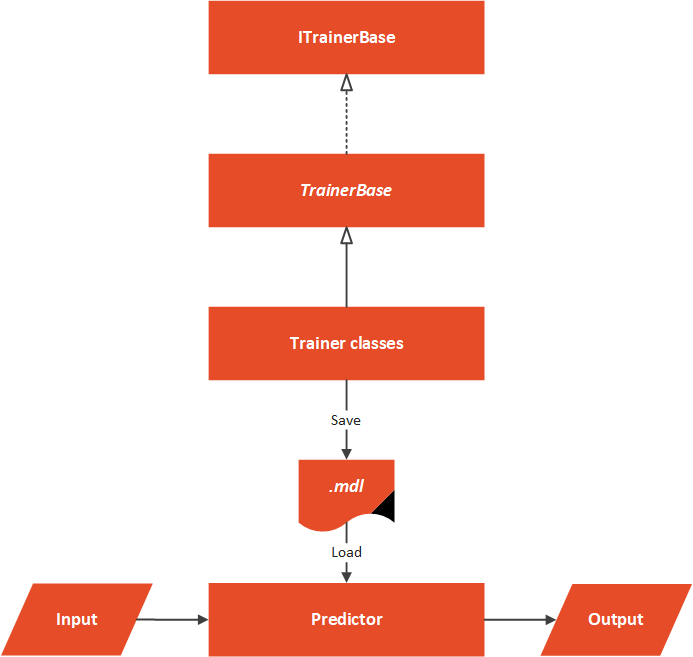
At the core of this solution, we have an abstract TrainerBase class. This class is in the Common folder and its main goal is to standardize the way this whole process is done. It is in this class where we process data and perform feature engineering. This class is also in charge of training machine learning algorithm. The classes that implement this abstract class are located in the Trainers folder. Here we can find multiple classes which utilize ML.NET algorithms. These classes define which algorithm should be used. In this particular case, we have only one Predictor located in the Predictor folder.
4.2 Data Models
In order to load data from the dataset and use it with ML.NET algorithms, we need to implement classes that are going to model this data. Two files can be found in Data Folder: PalmerPenguinBinaryData and PricePalmerPenguinBinaryPredictions. The PalmerPenguinBinaryData class models input data and it looks like this:
using Microsoft.ML.Data;
namespace DecisionTreeBinaryClassification.MachineLearning.DataModels
{
/// <summary>
/// Models Palmer Penguins Binary Data.
/// </summary>
public class PalmerPenguinsBinaryData
{
[LoadColumn(1)]
public bool Label { get; set; }
[LoadColumn(2)]
public float CulmenLength { get; set; }
[LoadColumn(3)]
public float CulmenDepth { get; set; }
}
}

The PricePalmerPenguinBinaryPredictions class models output data:
using Microsoft.ML.Data;
namespace DecisionTreeBinaryClassification.MachineLearning.DataModels
{
/// <summary>
/// Models Palmer Penguins Binary Prediction.
/// </summary>
public class PalmerPenguinsBinaryPrediction
{
public bool PredictedLabel { get; set; }
}
}
4.3 TrainerBase and ITrainerBase
As we mentioned, this class is the core of this implementation. In essence, there are two parts to it. The first one is the interface that describes this class and another is the abstract class that needs to be overridden with the concrete implementations, however, it implements interface methods. Here is the ITrainerBase interface:
using Microsoft.ML.Data;
namespace DecisionTreeBinaryClassification.MachineLearning.Common
{
public interface ITrainerBase
{
string Name { get; }
void Fit(string trainingFileName);
BinaryClassificationMetrics Evaluate();
void Save();
}
}The TrainerBase class implements this interface. However, it is abstract since we want to inject specific algorithms:
using DecisionTreeBinaryClassification.MachineLearning.DataModels;
using Microsoft.ML;
using Microsoft.ML.Calibrators;
using Microsoft.ML.Data;
using Microsoft.ML.Trainers;
using Microsoft.ML.Transforms;
using System;
using System.IO;
namespace DecisionTreeBinaryClassification.MachineLearning.Common
{
/// <summary>
/// Base class for Trainers.
/// This class exposes methods for training, evaluating and saving ML Models.
/// Classes that inherit this class need to assing concrete model and name.
/// </summary>
public abstract class TrainerBase<TParameters> : ITrainerBase
where TParameters : class
{
public string Name { get; protected set; }
protected static string ModelPath => Path
.Combine(AppContext.BaseDirectory, "classification.mdl");
protected readonly MLContext MlContext;
protected DataOperationsCatalog.TrainTestData _dataSplit;
protected ITrainerEstimator<BinaryPredictionTransformer<TParameters>, TParameters> _model;
protected ITransformer _trainedModel;
protected TrainerBase()
{
MlContext = new MLContext(111);
}
/// <summary>
/// Train model on defined data.
/// </summary>
/// <param name="trainingFileName"></param>
public void Fit(string trainingFileName)
{
if (!File.Exists(trainingFileName))
{
throw new FileNotFoundException($"File {trainingFileName} doesn't exist.");
}
_dataSplit = LoadAndPrepareData(trainingFileName);
var dataProcessPipeline = BuildDataProcessingPipeline();
var trainingPipeline = dataProcessPipeline.Append(_model);
_trainedModel = trainingPipeline.Fit(_dataSplit.TrainSet);
}
/// <summary>
/// Evaluate trained model.
/// </summary>
/// <returns>Model performance.</returns>
public BinaryClassificationMetrics Evaluate()
{
var testSetTransform = _trainedModel.Transform(_dataSplit.TestSet);
return MlContext.BinaryClassification.EvaluateNonCalibrated(testSetTransform);
}
/// <summary>
/// Save Model in the file.
/// </summary>
public void Save()
{
MlContext.Model.Save(_trainedModel, _dataSplit.TrainSet.Schema, ModelPath);
}
/// <summary>
/// Feature engeneering and data pre-processing.
/// </summary>
/// <returns>Data Processing Pipeline.</returns>
private EstimatorChain<NormalizingTransformer> BuildDataProcessingPipeline()
{
var dataProcessPipeline = MlContext.Transforms.Concatenate("Features",
nameof(PalmerPenguinsBinaryData.CulmenDepth),
nameof(PalmerPenguinsBinaryData.CulmenLength)
)
.Append(MlContext.Transforms.NormalizeMinMax("Features", "Features"))
.AppendCacheCheckpoint(MlContext);
return dataProcessPipeline;
}
private DataOperationsCatalog.TrainTestData LoadAndPrepareData(string trainingFileName)
{
var trainingDataView = MlContext.Data
.LoadFromTextFile<PalmerPenguinsBinaryData>
(trainingFileName, hasHeader: true, separatorChar: ',');
return MlContext.Data.TrainTestSplit(trainingDataView, testFraction: 0.3);
}
}
}

That is one large class. It controls the whole process. Let’s split it up and see what it is all about. First, let’s observe the fields and properties of this class:
public string Name { get; protected set; }
protected static string ModelPath => Path.Combine(AppContext.BaseDirectory, "classification.mdl");
protected readonly MLContext MlContext;
protected DataOperationsCatalog.TrainTestData _dataSplit;
protected ITrainerEstimator<BinaryPredictionTransformer<TParameters>, TParameters> _model;
protected ITransformer _trainedModel;The Name property is used by the class that inherits this one to add the name of the algorithm. The ModelPath field is there to define where we will store our model once it is trained. Note that the file name has .mdl extension. Then we have our MlContext so we can use ML.NET functionalities. Don’t forget that this class is a singleton, so there will be only one in our solution. The _dataSplit field contains loaded data. Data is split into train and test datasets within this structure.
The field _model is used by the child classes. These classes define which machine learning algorithm is used in this field. The _trainedModel field is the resulting model that should be evaluated and saved. In essence, the only job of the class that inherits and implements this one is to define the algorithm that should be used, by instantiating an object of the desired algorithm as _model.
Cool, let’s now explore Fit() method:
public void Fit(string trainingFileName)
{
if (!File.Exists(trainingFileName))
{
throw new FileNotFoundException($"File {trainingFileName} doesn't exist.");
}
_dataSplit = LoadAndPrepareData(trainingFileName);
var dataProcessPipeline = BuildDataProcessingPipeline();
var trainingPipeline = dataProcessPipeline.Append(_model);
_trainedModel = trainingPipeline.Fit(_dataSplit.TrainSet);
}This method is the blueprint for the training of the algorithms. As an input parameter, it receives the path to the .csv file. After we confirm that the file exists we use the private method LoadAndPrepareData. This method loads data into memory and splits it into two datasets, train and test dataset. We store the returning value into _dataSplit because we need a test dataset for the evaluation phase. Then we call BuildDataProcessingPipeline().

This is the method that performs data pre-processing and feature engineering. For this data, there is no need for some heavy work, we just do the normalization. Here is the method:
private EstimatorChain<NormalizingTransformer> BuildDataProcessingPipeline()
{
var dataProcessPipeline = MlContext.Transforms.Concatenate("Features",
nameof(PalmerPenguinsBinaryData.CulmenDepth),
nameof(PalmerPenguinsBinaryData.CulmenLength)
)
.Append(MlContext.Transforms.NormalizeMinMax("Features", "Features"))
.AppendCacheCheckpoint(MlContext);
return dataProcessPipeline;
}Next is the Evaluate() method:
public RegressionMetrics Evaluate()
{
var testSetTransform = _trainedModel.Transform(_dataSplit.TestSet);
return MlContext.Regression.Evaluate(testSetTransform);
}It is a pretty simple method that creates a Transformer object by using _trainedModel and test Dataset. Then we utilize MlContext to retrieve regression metrics. Finally, let’s check out Save() method:
public void Save()
{
MlContext.Model.Save(_trainedModel, _dataSplit.TrainSet.Schema, ModelPath);
}This is another simple method that just uses MLContext to save the model into the defined path.
4.4 Trainers
Thanks to all the heavy lifting that we have done in the TrainerBase class, the other Trainer classes are pretty simple and focused only on instantiating the ML.NET algorithm. We have two classes that utilize ML.NET‘s binary Decision Tree classifiers. Let’ take a look at DecisionTreeTrainer class:
using DecisionTreeBinaryClassification.MachineLearning.Common;
using Microsoft.ML;
using Microsoft.ML.Calibrators;
using Microsoft.ML.Trainers.FastTree;
namespace DecisionTreeBinaryClassification.MachineLearning.Trainers
{
public class DecisionTreeTrainer : TrainerBase<
CalibratedModelParametersBase<FastTreeBinaryModelParameters, PlattCalibrator>>
{
public DecisionTreeTrainer(int numberOfLeaves, int numberOfTrees, double learningRate = 0.2)
: base()
{
Name = $"Decision Tree-{numberOfLeaves}-{numberOfTrees}-{learningRate}";
_model = MlContext.BinaryClassification.Trainers.FastTree(numberOfLeaves: numberOfLeaves,
numberOfTrees: numberOfTrees,
learningRate: learningRate);
}
}
}As you can see, this class is pretty simple. We override the Name and _model. We use the FastTree class from the BinaryClassificaton namespace. Notice how we use some of the hyperparameters that this algorithm provides. With this, we can create more experiments. The numberOfLeaves represents the number of nodes that are going to be created in each branch of the decision tree, while the numberOfTrees represent the number of trees that are going to be trained. Remember, this implementation uses the MART algorithm, which creates multiple trees and then picks the best one. The learningRate hyperparameter defines how fast this algorithm learns. The other class, GamTrainer is even more simple:
using DecisionTreeBinaryClassification.MachineLearning.Common;
using Microsoft.ML;
using Microsoft.ML.Calibrators;
using Microsoft.ML.Trainers.FastTree;
namespace DecisionTreeBinaryClassification.MachineLearning.Trainers
{
public class GamTrainer : TrainerBase<
CalibratedModelParametersBase<GamBinaryModelParameters, PlattCalibrator>>
{
public GamTrainer() : base()
{
Name = "GAM";
_model = MlContext.BinaryClassification.Trainers.Gam();
}
}
}
No hyperparameters are used with this algorithm.
4.5 Predictor
The Predictor class is here to load the saved model and run some predictions. Usually, this class is not a part of the same microservice as trainers. We usually have one microservice that is performing the training of the model. This model is saved into file, from which the other model loads it and run predictions based on the user input. Here is how this class looks like:
public class Predictor
{
protected static string ModelPath => Path.Combine(AppContext.BaseDirectory, "svm.mdl");
private readonly MLContext _mlContext;
private ITransformer _model;
public Predictor()
{
_mlContext = new MLContext(111);
}
/// <summary>
/// Runs prediction on new data.
/// </summary>
/// <param name="newSample">New data sample.</param>
/// <returns>An object which contains predictions made by model.</returns>
public PalmerPenguinsBinaryPrediction Predict(PalmerPenguinsBinaryData newSample)
{
LoadModel();
var predictionEngine = _mlContext.Model.
CreatePredictionEngine<PalmerPenguinsBinaryData, PalmerPenguinsBinaryPrediction>(_model);
return predictionEngine.Predict(newSample);
}
private void LoadModel()
{
if (!File.Exists(ModelPath))
{
throw new FileNotFoundException($"File {ModelPath} doesn't exist.");
}
using (var stream = new FileStream(ModelPath,
FileMode.Open,
FileAccess.Read,
FileShare.Read))
{
_model = _mlContext.Model.Load(stream, out _);
}
if (_model == null)
{
throw new Exception($"Failed to load Model");
}
}
}In a nutshell, the model is loaded from a defined file, and predictions are made on the new sample. Note that we need to create PredictionEngine to do so.
4.6 Usage and Results
Ok, let’s put all of this together.
using DecisionTreeBinaryClassification.MachineLearning.Common;
using DecisionTreeBinaryClassification.MachineLearning.DataModels;
using DecisionTreeBinaryClassification.MachineLearning.Predictors;
using DecisionTreeBinaryClassification.MachineLearning.Trainers;
using System;
using System.Collections.Generic;
namespace DecisionTreeBinaryClassification
{
class Program
{
static void Main(string[] args)
{
var newSample = new PalmerPenguinsBinaryData
{
CulmenDepth = 1.2f,
CulmenLength = 1.1f
};
var trainers = new List<ITrainerBase>
{
new DecisionTreeTrainer(5, 10),
new DecisionTreeTrainer(5, 10, 0.1),
new DecisionTreeTrainer(10, 20),
new DecisionTreeTrainer(10, 20, 0.1),
new GamTrainer()
};
trainers.ForEach(t => TrainEvaluatePredict(t, newSample));
}
static void TrainEvaluatePredict(ITrainerBase trainer, PalmerPenguinsBinaryData newSample)
{
Console.WriteLine("*******************************");
Console.WriteLine($"{ trainer.Name }");
Console.WriteLine("*******************************");
trainer.Fit(.\\Data\\penguins_binary.csv");
var modelMetrics = trainer.Evaluate();
Console.WriteLine($"Accuracy: {modelMetrics.Accuracy:0.##}{Environment.NewLine}" +
$"F1 Score: {modelMetrics.F1Score:#.##}{Environment.NewLine}" +
$"Positive Precision: {modelMetrics.PositivePrecision:#.##}{Environment.NewLine}" +
$"Negative Precision: {modelMetrics.NegativePrecision:0.##}{Environment.NewLine}" +
$"Positive Recall: {modelMetrics.PositiveRecall:#.##}{Environment.NewLine}" +
$"Negative Recall: {modelMetrics.NegativeRecall:#.##}{Environment.NewLine}" +
$"Area Under Precision Recall Curve: {modelMetrics.AreaUnderPrecisionRecallCurve:#.##}{Environment.NewLine}");
trainer.Save();
var predictor = new Predictor();
var prediction = predictor.Predict(newSample);
Console.WriteLine("------------------------------");
Console.WriteLine($"Prediction: {prediction.PredictedLabel:#.##}");
Console.WriteLine("------------------------------");
}
}
}
Not the TrainEvaluatePredict() method. This method does the heavy lifting here. In this method, we can inject an instance of the class that inherits TrainerBase and a new sample that we want to be predicted. Then we call Fit() method to train the algorithm. Then we call Evaluate() method and print out the metrics. Finally, we save the model. Once that is done, we create an instance of Predictor, call Predict() method with a new sample and print out the predictions. In the Main, we create a list of trainer objects, and then we call TrainEvaluatePredict on these objects.
In the list of algorithms, we relied on the hyperparameters to create several variations of Decision Trees. Here are the results:
*******************************
Decision Tree-5-10-0.2
*******************************
Accuracy: 0.97
F1 Score: .97
Positive Precision: .96
Negative Precision: 0.98
Positive Recall: .98
Negative Recall: .96
Area Under Precision Recall Curve: .99
------------------------------
Prediction: True
------------------------------
*******************************
Decision Tree-5-10-0.1
*******************************
Accuracy: 0.97
F1 Score: .97
Positive Precision: .96
Negative Precision: 0.98
Positive Recall: .98
Negative Recall: .96
Area Under Precision Recall Curve: 1
------------------------------
Prediction: True
------------------------------
*******************************
Decision Tree-10-20-0.2
*******************************
Accuracy: 0.98
F1 Score: .98
Positive Precision: .98
Negative Precision: 0.98
Positive Recall: .98
Negative Recall: .98
Area Under Precision Recall Curve: 1
------------------------------
Prediction: True
------------------------------
*******************************
Decision Tree-10-20-0.1
*******************************
Accuracy: 0.97
F1 Score: .97
Positive Precision: .96
Negative Precision: 0.98
Positive Recall: .98
Negative Recall: .96
Area Under Precision Recall Curve: 1
------------------------------
Prediction: True
------------------------------
*******************************
GAM
*******************************
Accuracy: 0.96
F1 Score: .96
Positive Precision: .94
Negative Precision: 0.98
Positive Recall: .98
Negative Recall: .95
Area Under Precision Recall Curve: .99
------------------------------
Prediction: True
------------------------------Awesome, so we got different predictions from different algorithms, along with different metrics. All versions gave the correct answer since for the sample we provided we used one of the Adelie instances. Metrics give us the feeling that the Decision Tree with 5 leaves and a learning rate of 0.2 performs the best. This should be of course taken with a grain of salt and further test the model.
5. Regression Implementation with ML.NET
As we mentioned, for the regression example, we use Boston Housing Dataset. Here is how that looks like:

Most of the features in the dataset have almost linear dependency:

From the high-level, architecture stays the same. There are, of course, some changes in each concrete implementation, however the architecture is intact.

The same goes for the project structure:
5.1 Data Models
Just like in classification examples we need to create classes for data. Two classescan be found in Data Folder: BostonHousingData and BostonHousingPricePredictions. The BostonHousingData class models input data and it looks like this:
using Microsoft.ML.Data;
namespace DecisionTreeRegression.MachineLearning.DataModels
{
/// <summary>
/// Models Boston Housing Data.
/// </summary>
public class BostonHousingData
{
[LoadColumn(0)]
public float CrimeRate { get; set; }
[LoadColumn(1)]
public float Zoned { get; set; }
[LoadColumn(2)]
public float Proportion { get; set; }
[LoadColumn(3)]
public float RiverCoast { get; set; }
[LoadColumn(4)]
public float NOConcetration { get; set; }
[LoadColumn(5)]
public float NumOfRoomsPerDwelling { get; set; }
[LoadColumn(6)]
public float Age { get; set; }
[LoadColumn(7)]
public float EmployCenterDistance { get; set; }
[LoadColumn(8)]
public float HighwayAccecabilityRadius { get; set; }
[LoadColumn(9)]
public float TaxRate { get; set; }
[LoadColumn(10)]
public float PTRatio { get; set; }
[LoadColumn(11)]
public float MedianPrice { get; set; }
}
}
The BostonHousingPricePredictions class models output data:
using Microsoft.ML.Data;
namespace DecisionTreeRegression.MachineLearning.DataModels
{
/// <summary>
/// Models Boston Housing Prediction.
/// </summary>
public class BostonHousingPricePredictions
{
[ColumnName("Score")]
public float MedianPrice;
}
}5.2 TrainerBase and ITrainerBase
The ITranierBase interface is the same as in the classification example.
using Microsoft.ML.Data;
namespace DecisionTreeRegression.MachineLearning.Common
{
public interface ITrainerBase
{
string Name { get; }
void Fit(string trainingFileName);
RegressionMetrics Evaluate();
void Save();
}
}
The TranierBase implementation is at the center of the solution once again. It resembles the implementation we have done for classification example, however, there are some differences and specifics, since this class is adapted for regression and for specific data.
using DecisionTreeRegression.MachineLearning.DataModels;
using Microsoft.ML;
using Microsoft.ML.Data;
using Microsoft.ML.Trainers;
using Microsoft.ML.Transforms;
using System;
using System.IO;
namespace DecisionTreeRegression.MachineLearning.Common
{
/// <summary>
/// Base class for Trainers.
/// This class exposes methods for training, evaluating and saving ML Models.
/// Classes that inherit this class need to assing concrete model and name; and to implement data pre-processing.
/// </summary>
public abstract class TrainerBase<TParameters> : ITrainerBase
where TParameters : class
{
public string Name { get; protected set; }
protected static string ModelPath => Path.Combine(AppContext.BaseDirectory, "regression.mdl");
protected readonly MLContext MlContext;
protected DataOperationsCatalog.TrainTestData _dataSplit;
protected ITrainerEstimator<RegressionPredictionTransformer<TParameters>, TParameters> _model;
protected ITransformer _trainedModel;
protected TrainerBase()
{
MlContext = new MLContext(111);
}
/// <summary>
/// Train model on defined data.
/// </summary>
/// <param name="trainingFileName"></param>
public void Fit(string trainingFileName)
{
if (!File.Exists(trainingFileName))
{
throw new FileNotFoundException($"File {trainingFileName} doesn't exist.");
}
_dataSplit = LoadAndPrepareData(trainingFileName);
var dataProcessPipeline = BuildDataProcessingPipeline();
var trainingPipeline = dataProcessPipeline.Append(_model);
_trainedModel = trainingPipeline.Fit(_dataSplit.TrainSet);
}
/// <summary>
/// Evaluate trained model.
/// </summary>
/// <returns>RegressionMetrics object.</returns>
public RegressionMetrics Evaluate()
{
var testSetTransform = _trainedModel.Transform(_dataSplit.TestSet);
return MlContext.Regression.Evaluate(testSetTransform);
}
/// <summary>
/// Save Model in the file.
/// </summary>
public void Save()
{
MlContext.Model.Save(_trainedModel, _dataSplit.TrainSet.Schema, ModelPath);
}
/// <summary>
/// Feature engeneering and data pre-processing.
/// </summary>
/// <returns>Data Processing Pipeline.</returns>
private EstimatorChain<NormalizingTransformer> BuildDataProcessingPipeline()
{
var dataProcessPipeline = MlContext.Transforms.CopyColumns("Label", nameof(BostonHousingData.MedianPrice))
.Append(MlContext.Transforms.Categorical.OneHotEncoding("RiverCoast"))
.Append(MlContext.Transforms.Concatenate("Features",
"CrimeRate",
"Zoned",
"Proportion",
"RiverCoast",
"NOConcetration",
"NumOfRoomsPerDwelling",
"Age",
"EmployCenterDistance",
"HighwayAccecabilityRadius",
"TaxRate",
"PTRatio"))
.Append(MlContext.Transforms.NormalizeLogMeanVariance("Features", "Features"))
.AppendCacheCheckpoint(MlContext);
return dataProcessPipeline;
}
private DataOperationsCatalog.TrainTestData LoadAndPrepareData(string trainingFileName)
{
var trainingDataView = MlContext.Data.LoadFromTextFile<BostonHousingData>(trainingFileName, hasHeader: true, separatorChar: ',');
return MlContext.Data.TrainTestSplit(trainingDataView, testFraction: 0.3);
}
}
}
The most notable changes are in the BuildDataProcessingPipeline. In this function, we have done some data pre-processing and feature engineering. Namely, we used one-hot encoding on the RiverCoast feature and used log mean normalization on all features.
private EstimatorChain<NormalizingTransformer> BuildDataProcessingPipeline()
{
var dataProcessPipeline = MlContext.Transforms.CopyColumns("Label",
nameof(BostonHousingData.MedianPrice))
.Append(MlContext.Transforms.Categorical.OneHotEncoding("RiverCoast"))
.Append(MlContext.Transforms.Concatenate("Features",
"CrimeRate",
"Zoned",
"Proportion",
"RiverCoast",
"NOConcetration",
"NumOfRoomsPerDwelling",
"Age",
"EmployCenterDistance",
"HighwayAccecabilityRadius",
"TaxRate",
"PTRatio"))
.Append(MlContext.Transforms.NormalizeLogMeanVariance("Features", "Features"))
.AppendCacheCheckpoint(MlContext);
return dataProcessPipeline;
}5.3 Trainers
In the trainer’s folder, we can find three classes. In addition to Fast Tree and GAM, we now utilize and Fast Tree Tweedie algorithm. Fast Tree and GAM are almost the same as in the classification example. The only difference is that we use classes from the Regression namespace.
using DecisionTreeRegression.MachineLearning.Common;
using Microsoft.ML;
using Microsoft.ML.Trainers.FastTree;
namespace DecisionTreeRegression.MachineLearning.Trainers
{
/// <summary>
/// Class that uses Decision Tree algorithm.
/// </summary>
public sealed class DecisionTreeTrainer : TrainerBase<FastTreeRegressionModelParameters>
{
public DecisionTreeTrainer(int numberOfLeaves, int numberOfTrees, double learningRate = 0.2)
: base()
{
Name = $"Decision Tree-{numberOfLeaves}-{numberOfTrees}-{learningRate}";
_model = MlContext.Regression.Trainers.FastTree(numberOfLeaves: numberOfLeaves,
numberOfTrees: numberOfTrees,
learningRate: learningRate);
}
}
}
using DecisionTreeRegression.MachineLearning.Common;
using Microsoft.ML;
using Microsoft.ML.Trainers.FastTree;
namespace DecisionTreeRegression.MachineLearning.Trainers
{
/// <summary>
/// Class that uses Decision Tree algorithm.
/// </summary>
public sealed class GamTrainer : TrainerBase<GamRegressionModelParameters>
{
public GamTrainer() : base()
{
Name = $"GAM";
_model = MlContext.Regression.Trainers.Gam();
}
}
}

The additional FastTreeTweedieTrainer is straightforward too:
using DecisionTreeRegression.MachineLearning.Common;
using Microsoft.ML;
using Microsoft.ML.Trainers.FastTree;
namespace DecisionTreeRegression.MachineLearning.Trainers
{
/// <summary>
/// Class that uses Fast Tree Twidie algorithm.
/// </summary>
public sealed class FastTreeTweedieTrainer : TrainerBase<FastTreeTweedieModelParameters>
{
public FastTreeTweedieTrainer(int numberOfLeaves,
int numberOfTrees,
double learningRate = 0.2)
: base()
{
Name = $"Fast Tree Tweedie-{numberOfLeaves}-{numberOfTrees}-{learningRate}";
_model = MlContext.Regression.Trainers.FastTreeTweedie(numberOfLeaves: numberOfLeaves,
numberOfTrees: numberOfTrees,
learningRate: learningRate);
}
}
}
It uses the same hyperparameters as FastTree implementation.
5.4 Predictor
The Predictor class is also adopted for this scenario:
using DecisionTreeRegression.MachineLearning.DataModels;
using Microsoft.ML;
using System;
using System.IO;
namespace DecisionTreeRegression.MachineLearning.Predictors
{
/// <summary>
/// Loads Model from the file and makes predictions.
/// </summary>
public class Predictor
{
protected static string ModelPath => Path.Combine(AppContext.BaseDirectory, "regression.mdl");
private readonly MLContext _mlContext;
private ITransformer _model;
public Predictor()
{
_mlContext = new MLContext(111);
}
/// <summary>
/// Runs prediction on new data.
/// </summary>
/// <param name="newSample">New data sample.</param>
/// <returns>BostonHousingPricePredictions object.</returns>
public BostonHousingPricePredictions Predict(BostonHousingData newSample)
{
LoadModel();
var predictionEngine = _mlContext.Model.CreatePredictionEngine<
BostonHousingData, BostonHousingPricePredictions>(_model);
return predictionEngine.Predict(newSample);
}
private void LoadModel()
{
if (!File.Exists(ModelPath))
{
throw new FileNotFoundException($"File {ModelPath} doesn't exist.");
}
using (var stream = new FileStream(ModelPath,
FileMode.Open,
FileAccess.Read,
FileShare.Read))
{
_model = _mlContext.Model.Load(stream, out _);
}
if (_model == null)
{
throw new Exception($"Failed to load Model");
}
}
}
}

7.4 Usage and Results
Let’s see how this works together:
using DecisionTreeRegression.MachineLearning.Common;
using DecisionTreeRegression.MachineLearning.DataModels;
using DecisionTreeRegression.MachineLearning.Predictors;
using DecisionTreeRegression.MachineLearning.Trainers;
using System;
using System.Collections.Generic;
namespace DecisionTreeRegression
{
class Program
{
static void Main(string[] args)
{
var newSample = new BostonHousingData
{
Age = 65.2f,
CrimeRate = 0.00632f,
EmployCenterDistance = 4.0900f,
HighwayAccecabilityRadius = 15.3f,
NOConcetration = 0.538f,
NumOfRoomsPerDwelling = 6.575f,
Proportion = 1f,
PTRatio = 15.3f,
RiverCoast = 0f,
TaxRate = 296f,
Zoned = 23f
};
var trainers = new List<ITrainerBase>
{
new DecisionTreeTrainer(5, 10),
new DecisionTreeTrainer(5, 10, 0.1),
new DecisionTreeTrainer(10, 20),
new DecisionTreeTrainer(10, 20, 0.1),
new FastTreeTweedieTrainer(5, 10),
new FastTreeTweedieTrainer(5, 10, 0.1),
new FastTreeTweedieTrainer(10, 20),
new FastTreeTweedieTrainer(10, 20, 0.1),
new GamTrainer()
};
trainers.ForEach(t => TrainEvaluatePredict(t, newSample));
}
static void TrainEvaluatePredict(ITrainerBase trainer, BostonHousingData newSample)
{
Console.WriteLine("*******************************");
Console.WriteLine($"{ trainer.Name }");
Console.WriteLine("*******************************");
trainer.Fit(".\\Data\\boston_housing_dataset.csv");
var modelMetrics = trainer.Evaluate();
Console.WriteLine($"Loss Function: {modelMetrics.LossFunction:0.##}{Environment.NewLine}" +
$"Mean Absolute Error: {modelMetrics.MeanAbsoluteError:#.##}{Environment.NewLine}" +
$"Mean Squared Error: {modelMetrics.MeanSquaredError:#.##}{Environment.NewLine}" +
$"RSquared: {modelMetrics.RSquared:0.##}{Environment.NewLine}" +
$"Root Mean Squared Error: {modelMetrics.RootMeanSquaredError:#.##}");
trainer.Save();
var predictor = new Predictor();
var prediction = predictor.Predict(newSample);
Console.WriteLine("------------------------------");
Console.WriteLine($"Prediction: {prediction.MedianPrice:#.##}");
Console.WriteLine("------------------------------");
}
}
}
The output looks like this:
*******************************
Decision Tree-5-10-0.2
*******************************
Loss Function: 4.59
Mean Absolute Error: 1.93
Mean Squared Error: 4.59
RSquared: 0.07
Root Mean Squared Error: 2.14
------------------------------
Prediction: 14.55
------------------------------
*******************************
Decision Tree-5-10-0.1
*******************************
Loss Function: 41.23
Mean Absolute Error: 6.27
Mean Squared Error: 41.23
RSquared: -7.32
Root Mean Squared Error: 6.42
------------------------------
Prediction: 9.79
------------------------------
*******************************
Decision Tree-10-20-0.2
*******************************
Loss Function: 0.6
Mean Absolute Error: .51
Mean Squared Error: .6
RSquared: 0.88
Root Mean Squared Error: .78
------------------------------
Prediction: 15.3
------------------------------
*******************************
Decision Tree-10-20-0.1
*******************************
Loss Function: 5.6
Mean Absolute Error: 2.21
Mean Squared Error: 5.6
RSquared: -0.13
Root Mean Squared Error: 2.37
------------------------------
Prediction: 13.23
------------------------------
*******************************
Fast Tree Tweedie-5-10-0.2
*******************************
Loss Function: 24.96
Mean Absolute Error: 4.82
Mean Squared Error: 24.96
RSquared: -4.04
Root Mean Squared Error: 5
------------------------------
Prediction: 11.46
------------------------------
*******************************
Fast Tree Tweedie-5-10-0.1
*******************************
Loss Function: 138.21
Mean Absolute Error: 11.6
Mean Squared Error: 138.21
RSquared: -26.9
Root Mean Squared Error: 11.76
------------------------------
Prediction: 5.68
------------------------------
*******************************
Fast Tree Tweedie-10-20-0.2
*******************************
Loss Function: 1.13
Mean Absolute Error: .85
Mean Squared Error: 1.13
RSquared: 0.77
Root Mean Squared Error: 1.06
------------------------------
Prediction: 14.09
------------------------------
*******************************
Fast Tree Tweedie-10-20-0.1
*******************************
Loss Function: 30.71
Mean Absolute Error: 5.38
Mean Squared Error: 30.71
RSquared: -5.2
Root Mean Squared Error: 5.54
------------------------------
Prediction: 10.4
------------------------------
*******************************
GAM
*******************************
Loss Function: 0.72
Mean Absolute Error: .61
Mean Squared Error: .72
RSquared: 0.85
Root Mean Squared Error: .85
------------------------------
Prediction: 17.45
------------------------------Conclusion
In this article, we covered a lot of ground. We learned how Decision Trees work and how are they built with the CART algorithm with the Gini impurity index. Also, we had a chance to see how it can be used for classification and for regression. As always, we implemented it all using ML.NET.
Thank you for reading!

Nikola M. Zivkovic
CAIO at Rubik's Code
Nikola M. Zivkovic a CAIO at Rubik’s Code and the author of book “Deep Learning for Programmers“. He is loves knowledge sharing, and he is experienced speaker. You can find him speaking at meetups, conferences and as a guest lecturer at the University of Novi Sad.
Rubik’s Code is a boutique data science and software service company with more than 10 years of experience in Machine Learning, Artificial Intelligence & Software development. Check out the services we provide.




Trackbacks/Pingbacks