Generative Adversarial Networks (GAN) has changed the way we observe deep learning field. Up until that point, generative algorithms were a one-side ally, and the engineers were focused more on regression and classification tasks. Different approaches and applications were used for generating data. However, Ian Goodfellow presented GAN back in 2014 and shook up the entire field. Little did he knew the idea that he got while drinking with his friends would make him famous (well, science famous, not Rihanna famous). Thanks to that idea we live in a world where art created with these systems are sold for thousands of dollars and realistic images faces are generated.
Today, we can find hundreds of variations of GAN too. I mean, just look at that linked list, it is huge! We are living in a weird postmodern world and I love it. Actually, the first time I saw Picasso-styled Space Odyssey was the moment that made me start exploring this vast world of neural networks. What we can see in that video is that someone used Picasso’s style and applied it to Space Odyssey. This experiment was not done with GANs back then, but today we have one interesting architecture on our hands that can do just that.
2001: A Picasso Odyssey – Source
Actually, in this article, we are going to explore the problem of merging two domains of data. For example, we might want to apply the Picasso style to the Kubrick experience, but what if we want to do something else and make Picasso’s work more Kubrick like? To be honest, I am not sure if we want to do that with late Cubanism, so this might be the wrong example. However, you get the picture (pun intended). We want to move a specific style of one domain to the other and do that in both directions. This type of problem is usually referred to as Image-to-Image translation.
In general, Image-to-image translation is a class of graphics problems where the goal is to learn how input image can be mapped to an output image. Regularly, we would have aligned image pairs of both image domains. For example, we would have Monet’s painting and the image of the landscape that he painted. However, this is not always the case, as you can see from the example – we don’t have images of the landscapes that Monet painted. So in this article, we will explore how we can translate an image from a domain X to a domain Y without paired examples.
So far we didn’t solve this kind of problems in our big artificial neural networks journey. In fact, during our work on GANs, we used different architectures to generate images. First, we used standard GAN and DCGAN on the Fashion-MNIST Dataset, and then we got a chance to get familiar with Adversarial Autoencoders and implemented it. These are all very good architectures, but they are not really applicable to our new problem. Transferring information between two domains of images is done with a special type of GANs – Cycle GAN (paper).
Arhitecture

Let’s start with the fact that we have two unrelated sets of images. One is a set of images of Novi Sad, the city I live in, and the other is a set of images of Nadezda Petrovic, a famous Serbian painter. We will call the first set of images domain X, and the other one domain Y. As you can see, the images are unrelated, so we have an unpaired set of training data. However, we want to do two things. We want to generate images that will apply Nadezda’s style to photographs of Novi Sad, and we want to make Nadezda’s paintings look more like photographs. Here lies the power of CycleGAN. They don’t need a one-to-one mapping between source domain X and target domain Y.

For this purpose, we will create two Generators G and F. The first one has the goal to map X domain to Y (G: X → Y), and the second one will have a goal to map Y domain to X (F: Y → X). These Generators will have their respective adversarial Discriminators Dy and Dx. Discriminator Dy forces generator G to transform inputs that come from domain X into outputs that will be indistinguishable from the images from domain Y. On the other hand, discriminator Dx forces generator F to map inputs from domain X into outputs that look like they are from domain Y. The entire architecture can be seen in the image below.

In addition to this, the process of mapping needs to be regularized, so the two-cycle consistency losses are introduced. These losses are making sure that if we translate an image to one domain to the other and back again, we will get the same(ish) image. These losses are called forward cycle-consistency loss (x → G(x) → F(G(x)) ≈ x), and backward cycle-consistency loss (y → F(y) → G(F(y)) ≈ y ). We will explore these more in the next section.
This cycle-consistency mechanism is not a new thing. In fact, this method is used for a long time in visual tracking and verifying and improving translations. Some forms of higher-order cycle-consistency are used for 3D shape matching, co-segmentation, depth estimation, etc. Using this mechanism, CycleGan is actually pushing its generators to be consistent with each other.
Generator
Let’s talk a little bit more about generators themselves since they are quite interesting. From the high level it consists of three parts:
- Encoder
- Transformator
- Decoder
This might remind you of the Adversarial Autoencoders or Autoencoders in general, and you would not be wrong. Here is how the whole generator would look:

The encoder is in charge of extracting features from an input image. This is, of course, done by using Convolutional Layers. Transformator uses these features and combines them. Then, based on them it makes a decision about how to transform that feature from one domain to another. For this ResNet Layers are usually used. These layers come from Residual Networks, hence the name, and they consist of two convolutional layers. However, these layers use the residual of the original input as well. Here is a scheme of how they look:

In general, these layers are used to regulate the relationship between encoder and decoder. They try to keep the characteristic of input objects, (size, shape…). The decoder uses deconvolutional layers to reverse the encoder process.
Math Behind the Idea

As mentioned in the previous chapter, we have two generators (G and F), and two discriminators (Dx, Dy). We can observe generators as mapping functions whose goal is to translate data from domain X into domain Y and vice versa. Training samples of domain X that can be defined as:

where xi ∈ X. Samples from domain Y are defined as:

Distribution for this data is defined as:
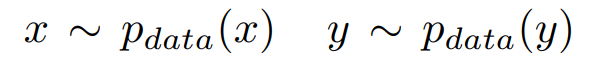
Essentially we have to define two types of loss:
- Adversarial loss
- Cycle-consistency loss
The adversarial loss is used to match the distribution of generated images and images from the target domain. This loss is applied to both generators. For the generator G that translates images from domain X to domain Y – G: X → Y, we define loss as follows:

As in standard GANs, generator G tries to generate images G(x) that look like images from domain Y. On the other hand, Dy tries to figure out where the image comes from: from G(x) or real dataset Y. G and D are playing the zero-sum game: minG maxDY LGAN(G, DY , X, Y ). This means that G tries to minimize this objective against Dy that tries to maximize it. For the generator F, we use a similar approach, only with discriminator Dx.
The Cycle-consistency loss pushes both generators to be consistent. It regulates them and adds additional stability to an otherwise quite unstable GAN’s training process. In theory, this system could work without this additional loss. However, generators can translate the same set of input images to any random permutation of images in the target domain, because technically their distribution would match. This means that adversarial loss is not enough. This loss is defined like this:

Cycle-consistency loss
So when we combine these losses, we end up with full objective:

where λ controls the relative importance of the two objectives. Finally, we are trying to solve:

Conclusion
In this article, we got familiar with the main concepts behind CycleGAN. We were able to explore its architecture, the math behind it, and get the overall theoretical knowledge about this type of GANs. In the next article, we will implement one solution that will be able to transform images from one domain to another.
Thank you for reading!
This article is a part of Artificial Neural Networks Series, which you can check out here.
Read more posts from the author at Rubik’s Code.




